Sometime over the past couple of months, as reality turned into a crash course in infectious disease epidemiology, you probably ran into the concept of herd immunity, that is, the point at which enough people are immune to the disease that it can no longer cause an explosive outbreak. The seemingly simple concept defines the ultimate exit strategy for the disease. But the reality of this tiny virus seems endlessly complex. A few recent papers have proposed a nuanced view of herd immunity that some will be sure to insist should be part of our plans for ending the lockdown. To understand the importance and limitations of this, we first need to dig deeper into the whole concept of herd immunity.
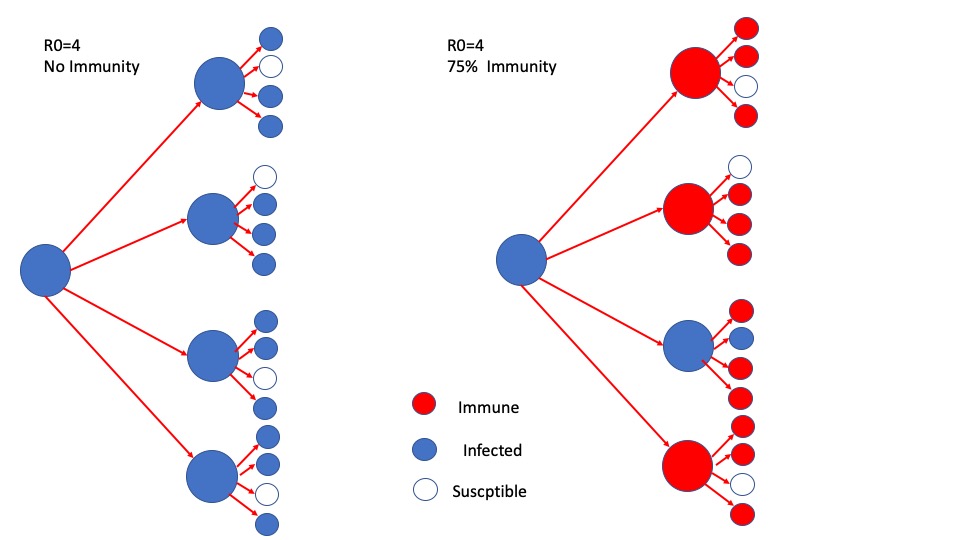
Let’s play a game called Contagion. The rules are simple. You start with a quarter, a timer, a Sharpie, and a mark on your forehead. You are now infected. Until that timer goes off, your job is to flip a coin every time you meet someone. If it’s heads, you mark their forehead and they get their own coin, timer, and Sharpie. How many people will you infect? If you meet eight people before the timer goes off, you can expect to infect four of them. That number is the initial reproduction number, R0, for your infection. As conditions change the reproduction number will change from that initial value, so we call it simply R.
As you might imagine, a disease with R0=4 will grow rapidly. Four cases, then 16, then 64, then 256 cases, then over a thousand. From a single case. But, as the game continues, players will eventually run into people who already have a mark on their head. Another rule in the game is that you can’t mark someone twice. We call those people playing with marks immune. That means that I will sometimes flip a coin, get heads, be ready to infect someone, and discover I can’t. If a quarter of the people I meet are immune, I will infect 3 instead of 4, so R drops. If half are immune, R becomes 2. If ¾ are immune, I would expect to infect only one new person, meaning the outbreak barely sustains itself and stops growing. That percentage, the level of herd immunity required to reduce R to one, defines what percent of people need to be immune to stop an outbreak from growing. The higher R0, the higher the percentage required to reach herd immunity. If R0 is 2.0, herd immunity occurs at 50%. 1 – ½ =50% (if you are going to infect two people, but half of them are immune, you infect one). If it’s 10, herd immunity occurs at 90%.
The simple formula is:
Herd immunity level = 1- 1/R0.
Try it. If R0=4, herd immunity occurs when two out of the three people you would have infected are immune. As a result, you infect only one. Put mathematically, 1 – 1/4 =3/4 or 75%.
The original notion of herd immunity referred to how many cows in a herd would need to be immune to stop a disease outbreak. The underlying assumption is that the cattle will do nothing to change their behavior. For the cattle herd, the only way to get immunity is either to become infected or to be vaccinated. Most of us are not cattle and can change our behavior. so, we have come up with other ways to reduce R. Our options are:
- If you are infected, we take you out of the game (quarantine you) before you can infect anyone. This has long been seen as the most cost-effective and efficient way to limit the spread of an infectious disease. If you can make it work. That requires that we know you are infected. The difficult thing about COVID-19 is that there is a long period during which you can infect people without anyone knowing you are infected. It’s as if these Sharpies have a special ink that stays invisible for days before anyone can see the mark. In fact, we now know that you can become infected, infect other people, and never develop symptoms. That means it is possible, even likely, that you have infected other people before your mark shows up. So, we not only need to lock you up, we also need to track down and lock up anyone you might have marked. That is called contact tracing. The earlier we can find you, the better. Hence the need for widespread testing.
- We can alter the chance that any given encounter causes an infection. People can stay out of arm’s reach to make it hard for you to mark them. Or they can put tape on their forehead. Face masks and social distancing rules are all about reducing the probability of infection for every encounter. Think of this as replacing your coin with a pair of dice and insisting that you roll snake eyes.
- We can act as if everyone is infected. If we don’t know who is infected, then the only way to reduce the number of contacts is to quarantine everyone. In particular, we want to remove people from crowded place where you might run in to dozens of people. Hence, the dreaded lockdowns and business closures.
To limit the impact of COVID-19, we need to use some combination of these three options until we somehow hit herd immunity. A recent paper made the case that R0 is not the same for everyone in the population. The argument goes that the spread of the disease is being driven by a small fraction of the population with high numbers of interactions, not only because this group is the most likely to spread infections, but also, because it is the most likely to become infected. To put this more complex model in mathematical terms, each of us has a different R0 and, if those with a high R0 become immune, R for the entire population will drop disproportionately. The model put forward in this paper suggests that we might be able to attain herd immunity with as little as 10% of the population infected. Estimates of R0 have ranged everywhere from 2.0 to 25, which, using the classic model, would call for anywhere from 50% to 96% of the population to be immune before herd immunity could be reached. It is possible that a lower number might be effective, particularly if some of the efforts to reduce R through behavioral change or through contact tracing and quarantine become routine, but I wouldn’t bet the farm on anything much below 50%.
The problem with this more nuanced model is that it is not nuanced enough. It does not recognize that the local population density and social structure play key roles in defining R values and that the risk of spread is defined as much or more by the environment as by the habits of any individual. Crowded cities have by far the highest R0. Cultures that don’t shake hands or hug will tend to have lower values of R0 across the population. Quiet homebodies might have a low R0 under most conditions, but if they ride the bus, they become super spreaders. The underlying point that we should think about heterogeneity in transmission is well taken and should remind us of the complexity of this pandemic. To some extent, the whole notion that we can define the response of a population with a single number is an artificial construct. R0 depends on so many different factors, from weather to population density to transportation infrastructure to cultural norms that the whole notion of estimating a specific number for a specific virus is inherently over simplistic and flawed. Whatever we do, we need to find a way to push the effective R for the population as far below 1.0 as possible using whatever tools are available until we have a vaccine or an effective treatment that could allow us to achieve herd immunity. We are not managing a model. We are managing reality and any effort to control this virus should include an element of overkill. Otherwise, one has a leading epidemiologist like Rush Limbaugh insisting that we have already reached herd immunity in California. When you hear that, watch out.


